问题描述:Fibonacci 数(Fibonacci Number)的定义是:F(n) = F(n - 1) + F(n - 2),并且 F(0) = 0,F(1) = 1。对于任意指定的整数 n(n ≥ 0),计算 F(n) 的精确值,并分析算法的时间、空间复杂度。
假设系统中已经提供任意精度长整数的运算,可以直接使用。
这其实是个老生常谈的问题了,不过可能在复杂度分析的时候,很多人忽略了一些事情。另外这个问题恰好有几种复杂度迥异的算法,在刚刚介绍完 算法复杂度 之后,正好来直观地理解一下。
一、递归法
一个看起来很直观、用起来很恐怖的算法就是递归法。根据 Fibonacci 的递推公式,对于输入的 n,直接递归地调用相同的函数分别求出 F(n - 1) 和 F(n - 2),二者相加就是结果。递归的终止点就是递推方程的初值,即 n 取 0 或 1 的时候。
程序(in Python)写出来那也是相当的简洁直观(为了跟后面的程序区分开来,这里取名 SlowFibonacci)。
1 2 3 4 | def SlowFibonacci(n):
assert n >= 0, 'invalid n'
if n < 2: return n # F(0) = 0, F(1) = 1
return SlowFibonacci(n - 1) + SlowFibonacci(n - 2)
|
这个算法的时间复杂度有着跟 Fibonacci 类似的递推方程:T(n) = T(n - 1) + T(n - 2) + O(1),很容易得到 T(n) = O(1.618 ^ n)(1.618 就是黄金分割,\((1+\sqrt5)/2\))。空间复杂度取决于递归的深度,显然是 O(n)。
二、递推法
虽然只是一字之差,但递推法的复杂度要小的多。这个方法就是按照递推方程,从 n = 0 和 n = 1 开始,逐个求出所有小于 n 的 Fibonacci 数,最后就可以算出 F(n)。由于每次计算值需要用到前两个 Fibonacci 数,更小的数就可以丢弃了,可以将空间复杂度降到最低。算法如下:
1 2 3 4 5 6 7 | def NormFibonacci(n):
assert n >= 0, 'invalid n'
if n == 0: return 0
(prev, curr) = (0, 1) # F(0), F(1)
for i in xrange(n - 1):
(prev, curr) = (curr, prev + curr)
return curr
|
显然时间复杂度是 O(n),空间复杂度是 O(1)。
比较一下递归法和递推法,二者都用了分治的思想——把目标问题拆为若干个小问题,利用小问题的解得到目标问题的解。二者的区别实际上就是普通分治算法和动态规划的区别。
三、矩阵法
算 Fibonacci 数精确值的最快的方法应该就是矩阵法,看过的人都觉得这个方法很好。如果你跟我一样,曾经为记住这个方法中的矩阵而烦恼,那今天就来看看怎么进行推导。其实方法非常简单,想清楚了也就自然而然地记住了。
我们把 Fibonacci 数列中相邻的两项:F(n) 和 F(n - 1) 写成一个 2x1 的矩阵,然后对其进行变形,看能得到什么:
是不是非常自然呢?把等式最右边继续算下去,最后得到:
因此要求 F(n),只要对这个二阶方阵求 n - 1 次方,最后取结果方阵第一行第一列的数字就可以了。
看起来有点儿化简为繁的感觉,但关键点在于,幂运算是可以二分加速的。设有一个方阵 a,利用分治法求 a 的 n 次方,有:
可见复杂度满足 T(n) = T(n / 2) + O(1),根据 Master 定理 可得:T(n) = O(log n)。
在实现的时候,可以用循环代替递归实现这里的二分分治,好处是降低了空间复杂度(用递归的话,空间复杂度为 O(log n))。下面的 Python 程序直接利用的 numpy 库中的矩阵乘法(当然这个库也实现了矩阵的幂运算,我把它单独写出来是为了强调这里的分治算法)。另外如果不用第三方库,我也给出了矩阵乘法的简单实现。
- Using numpy Library
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | from numpy import matrix
def MatrixPower(mat, n):
assert n > 0, 'invalid n'
res = None
temp = mat
while True:
if n & 1:
if res is None: res = temp
else: res = res * temp
n >>= 1
if n == 0: break
temp = temp * temp
return res
def FastFibonacci(n):
assert n >= 0, 'invalid n'
if n < 2: return n # F(0) = 0, F(1) = 1
mat = matrix([[1, 1], [1, 0]], dtype=object)
mat = MatrixPower(mat, n - 1)
return mat[0, 0]
|
- Without numpy Library
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | def DotProduct(x, y):
n = len(x)
assert len(y) == n, 'x and y must have the same length'
s = 0
for i in xrange(n):
s += x[i] * y[i]
return s
def MatrixMultiply(x, y):
# x is a m*a matrix, y is a a*n matrix.
# x * y is a m*n matrix.
m = len(x)
n = len(y[0])
a = len(x[0])
assert len(y) == a
# transpose y
y = [[y[i][j] for i in xrange(a)] for j in xrange(n)]
res = [[DotProduct(x[j], y[i]) for i in xrange(n)] for j in xrange(m)]
return res
def MatrixPower(mat, n):
assert n > 0, 'invalid n'
res = None
temp = mat
while True:
if n & 1:
if res is None: res = temp
else: res = MatrixMultiply(res, temp)
n >>= 1
if n == 0: break
temp = MatrixMultiply(temp, temp)
return res
def FastFibonacci(n):
assert n >= 0, 'invalid n'
if n < 2: return n # F(0) = 0, F(1) = 1
mat = [[1, 1], [1, 0]]
mat = MatrixPower(mat, n - 1)
return mat[0][0]
|
二阶方阵相乘一次可以看成是常数时间(虽然这个常数会比较大),因此整个算法的时间复杂度是 O(log n),空间复杂度是 O(1)。
四、运行时间大比拼
至此,我们得到的时间复杂度分别是 O(1.618 ^ n)、O(n) 和 O(log n) 的算法,让我们来直观地比较比较它们。
用 Python 的 timeit 模块对以上三个算法的运行时间进行了测量,记录了每个算法对于不同的 n 的每千次运算所消耗的时间(单位是秒),部分数据记录在 fibonacci_data。利用 Mathematica 可以很方便地对这些数据进行拟合,对于较小的 n,用三个复杂度表达式分别去拟合,得到的效果都非常好。尤其值得注意的是,对于第一个算法,我用 a * b ^ n 去拟合,结果得到 b 等于 1.61816,这与黄金分割数的正确值相差无几。
- 递归法拟合结果:0.000501741 * 1.61816 ^ n,RSquare = 0.999993。
- 递推法拟合结果:0.000788421 + 0.000115831 * n,RSquare = 0.999464。
- 矩阵法拟合结果:-0.0114923 + 0.0253609 log(n),RSquare = 0.986576。
下图是 n <= 35 时,三种算法的千次运行耗时比较。其中红色为 O(1.618 ^ n) 的递归法;蓝色为 O(n) 的递推法;绿色为 O(log n) 的矩阵法。散点为实际测量到的运行时间,实线为拟合方程的曲线。
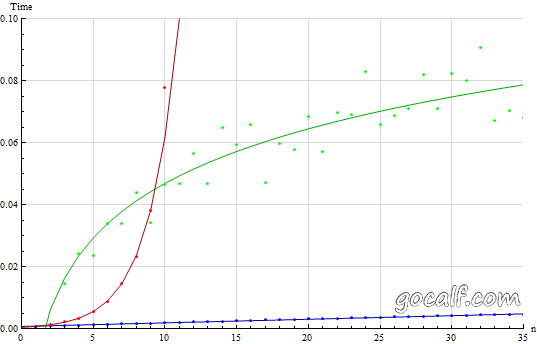
三种算法的运行时间比较
当 n > 10 的时候,指数时间就已经超出画面范围了。另外在这张图里,身为对数时间复杂度的矩阵法似乎没有任何优势,其耗时远远高于线性时间复杂度的递推法。这是因为 n 还不够大,体现不出 log(n) 的优势。在考虑更大的 n 之前,先来看看指数时间复杂度会增大到什么程度。
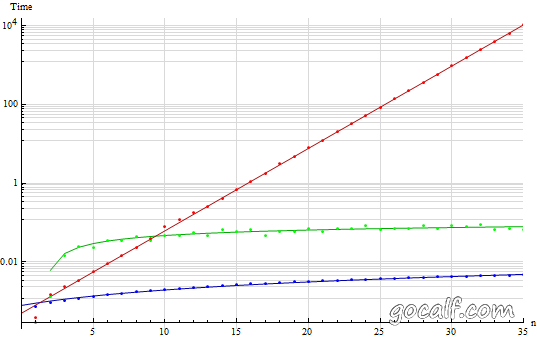
三种算法的运行时间比较(对数坐标轴)
五、大整数情况下的复杂度
Python 内置了大整数支持,因此上面的程序都可以直接接受任意大的 n。当整数在 32 位或 64 位以内时,加法和乘法都是常数时间,但大整数情况下,这个时间就不能忽略了。
先来看一下 Fibonacci 数的二进制位数。我们知道 Fibonacci 数的通项公式是:
当 n 充分大(其实都不需要很大)的时候,第二项就可以忽略不计了。把第一项对 2 取对数,就可以得到 Fibonacci 数的二进制位数的近似表达式,大概是 \(\log_2{1.618}\times n-0.5\log_2{5}=\log_2{1.618}\times n-1.161=O(n)\)。由此可以算出,F(47) 是 32 位无符号整数可以表达的最大的 Fibonacci 数,F(93) 是 64 位无符号整数可以表达的最大的 Fibonacci 数。上面图中的 n 在 36 以内,不需要动用大整数运算,复杂度也比较符合之前的结论。但对于更大的 n,之前的复杂度就不再适用了。
指数复杂度的算法就不管了,还不等用到大整数,它就已经慢到不行了。
来看看 O(n) 时间复杂度的递推法。每次递推的时候都要计算两个 Fibonacci 数之和,第 i 次运算时,这两个 Fibonacci 数分别有 O(i) 个二进制位,完成加法需要 O(i) 的时间。因此总的时间大约是:
可见对于很大的 n,递推法的时间复杂度实际上是 O(n ^ 2) 的,空间复杂度是 O(n) 用来存储 Fibonacci 数的各个二进制位。
再看矩阵法,注意到矩阵运算中有乘法,两个长度为 n 的大整数相乘,传统算法是 O(n ^ 2) 时间复杂度,较好的 Karatsuba 算法是 O(n ^ (log 3 / log 2)) 时间,更快的快速傅立叶变换法是 O(n log n) 时间。Python 2.5 中使用的是 Karatsuba 算法(Python 3 里面似乎是快速傅立叶变换法)(参见 Python 源码中的算法分析 之 大整数乘法)。以 Karatsuba 算法为例,矩阵法的时间复杂度递推方程为:\(T(n)=T(n/2)+O(n^{\log_2{3}})\),应用 Master 定理 求得 \(T(n)=O(n^{\log_2{3}})\)。因此对于很大的 n,矩阵法的时间复杂度为 O(n ^ 1.585),空间复杂度 O(n)。
利用 Mathematica 对大 n 情况下这两种算法每千次运行时间进行拟合,分别得到:
- 递推法大整数拟合结果:0.0131216 + 0.000102101 * n + 2.44765 * 10 ^ -7 * n ^ 2,RSquare = 0.999482。
- 矩阵法大整数拟合结果:0.171487 + 9.74496 * 10 ^ -7 * n ^ 1.51827,RSquare = 0.998395。
看一下 n 在 4000 以内时,两种复杂度的对比情况:
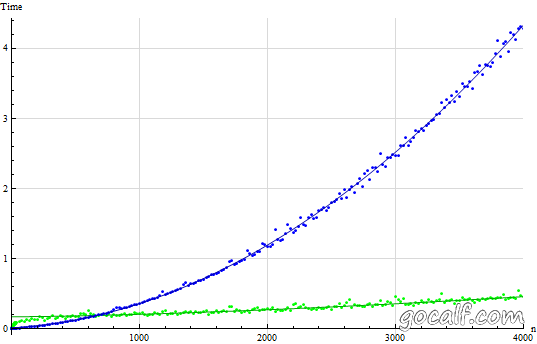
递推法(蓝色)与矩阵法(绿色)运行时间比较(大整数)
从图中可以看出,递推法的增长速度也是很快的,当 n 增大到 60 多的时候,它的运行时间就超过矩阵法了。矩阵法的增长速度非常慢,看起来像是线性的,让我们把 n 调的更大来看一下。
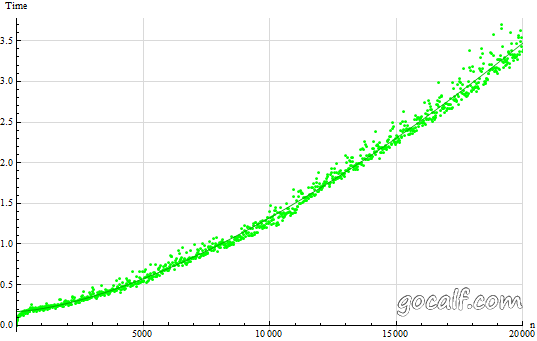
矩阵法的运行时间(更大的 n)
六、更快的算法?
试了试 Mathematica 中的 Fibonacci 函数,发现其运算速度相当惊人,估计时间复杂度在 O(n log n) 上下,而且对于相同的 n,运算速度远远高于我的矩阵法。可惜我还不了解它的算法,只是在帮助文档里看到:
Fibonacci[n] uses an iterative method based on the binary digit sequence of n.
来看看它到底有多快:
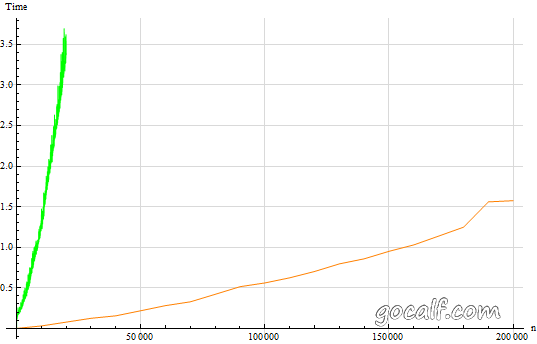
矩阵法(绿色)与 Mathematica Fibonacci 函数(橙色)运行时间比较
好吧,这个问题留待以后慢慢研究。
最后相关的 Mathematica 命令文件放在这里:fibonacci_timecost。
Comments
So what do you think? Did I miss something? Is any part unclear? Leave your comments below.